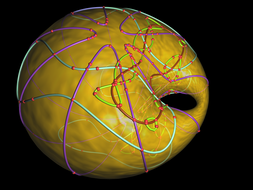
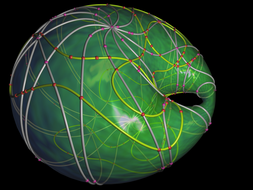
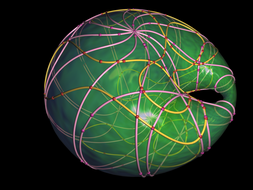
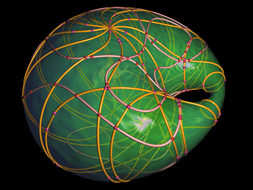
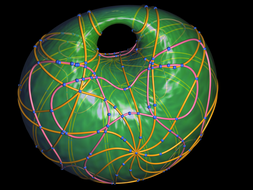
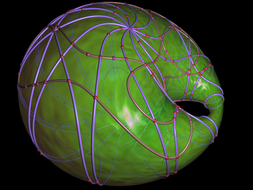
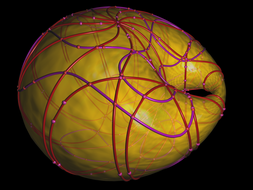
This project presents a set of curves rendered on the surface of a Dupin Cyclide. It was done together with my colleges from the Max-Planck Institute for Informatics. My part was essentially the rendering of plane algebraic curces (based on my Masters’s thesis) and OpenGL rendering of the surfaces. The rendered Dupin Cyclides looked so much cool that they were printed in the MPII calendar and also became a permanent logo of the “Algorithms and Complexity” research group. See also the publication list below.
Publication list
- A. Eigenwillig, M. Kerber: Exact and efficient 2D-arrangements of arbitrary algebraic curves. In: SODA 2008. ACM
- A. Eigenwillig, M. Kerber, N. Wolpert: Fast and exact geometric analysis of real algebraic plane curves. In: ISSAC 2007. DOI
- K. Mehlhorn, A. Eigenwillig, L. Kettner, W. Krandick, S. Schmitt, N. Wolpert: A Descartes Algorithms for Polynomials with Bit-Stream Coefficients. In: Reliable Implementation of Real Number Algorithms, 2005. DOI
- E. Berberich, M. Kerber: Exact arrangements on tori and Dupin cyclides. In: SPM 2008. DOI
- E. Berberich, M. Kerber, M. Sagraloff: Exact geometric-topological analysis of algebraic surfaces. In: SCG 2008. DOI
- E. Berberich, M. Sagraloff: A generic and flexible framework for the geometrical and topological analysis of (algebraic) surfaces. In: SMP 2008. DOI
- E. Berberich: Robust and efficient software for problems in 2.5-dimensional non-linear geometry: algorithms and implementations. PhD Thesis, 2008. DOI
- P. Emeliyanenko, E. Berberich, M. Sagraloff: Visualizing Arcs of Implicit Algebraic Curves, Exactly and Fast. In: ISCV 2009. DOI